Cracking the Code: Tips for Mastering Algebraic Equations
- Susan Ardila

- Jul 26, 2024
- 9 min read
Updated: Jul 2, 2025

Welcome, young scholars, parents, and math enthusiasts! Have you ever gazed at an algebraic equation and thought, “Is this a math problem or hieroglyphics?” Fear not! The world of algebra might seem like a riddle wrapped in an enigma, but with a little guidance, you’ll be solving equations like a seasoned pro—and maybe even having fun while doing it!
Math Vocabulary: Your Essential Toolbox
Before we dive into the magical land of algebra, let’s stock up on some essential gear. Understanding these key terms will provide you with the foundational knowledge you need to tackle any equation that comes your way.
Expression: A combination of numbers, variables, and operators (like (+) and (-)) with no equal sign. Think of it like a delicious math smoothie—just ingredients, no serving yet!
Equation: This is a full-course meal! An expression set equal to another expression (e.g., (3x + 4 = 10)). It’s where the fun begins!
Exponent: A tiny number that tells you how many times to use the base number in multiplication, like saying, “I want six slices of cake—not just one!”.
Coefficient: This is the number in front of a variable. In (4x), the coefficient is 4. It’s your trusty sidekick—always ready to help!
Constant: A number on its own, like the lone soldier, never changing while everything else shifts around it.
Variable: The mystic character marked by letters (commonly (x) or (y)). This is the variable hero of our story—the unknown!
Operation: What you do to numbers—add, subtract, multiply, or divide. Envision this as your math toolkit, each tool designated for a different task.
Inverse Operations: The opposites—addition and subtraction or multiplication and division. When one operation can undo another, like how a time-traveling device can rewind your awkward moments!
Eliminate: To remove a term from the equation. Consider it as decluttering your room; out with the old to make space for new!
Isolate: Getting that variable all alone on one side of the equation, like sending an introvert to a quiet corner.
Factor: Breaking down a number or expression into factors that can be multiplied. It’s the mysterious way to see how numbers are born.
Simplify: Cutting through the excess to make things easier to digest, akin to reducing your homework load—no one said math couldn’t be liberating!
Solve: Cracking the code of an equation to unveil the variable's true identity. It's like being a math detective, following the clues until you triumphantly reveal whodunit—or in this case, what-x-is!
Term: Individual parts of an expression separated by + or - signs. Each term is like a character in your equation’s story.
Commutative Property: This fancy term simply means that you can swap the order of numbers when adding or multiplying, and the result stays the same. For addition: 𝑎+𝑏=𝑏+𝑎. For multiplication: 𝑎×𝑏=𝑏×𝑎. It's like switching seats with your friend—you're still in the same classroom!
Associative Property: This property allows you to group numbers differently when adding or multiplying without changing the result. For addition: (𝑎+𝑏)+𝑐=𝑎+(𝑏+𝑐). For multiplication: (𝑎×𝑏)×𝑐=𝑎×(𝑏×𝑐). Think of it as rearranging your study group—no matter how you cluster, you're all still learning together!
These properties are like the secret handshakes of math—they give you the flexibility to rearrange numbers and expressions in ways that can make solving problems much easier. So next time you're tackling an equation, remember that you have the power to shuffle things around!
Remember PEMDAS!
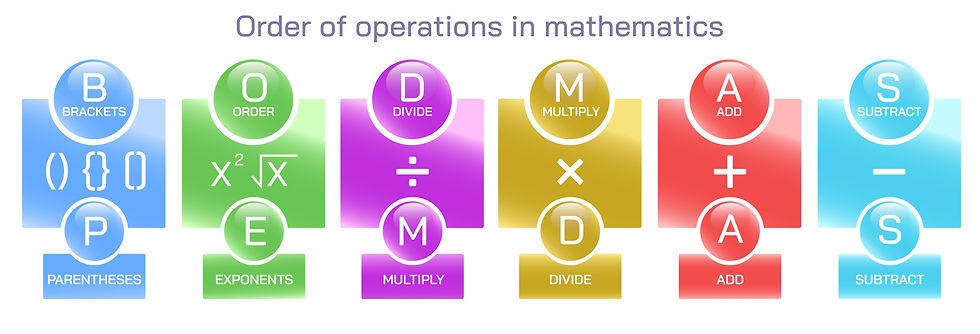
Before diving deeper, let’s talk about the mighty PEMDAS—an acronym to remember the order of operations:
P-arentheses, E-xponents, M-ultiplication, D-ivision, A-ddition, S-ubtraction. Think of PEMDAS as a traffic light guiding you through the busy intersection of mathematics. If you don’t follow it, you might end up crashing into chaos!
Example:
Solve 3+4×2
Multiply first: 4 × 2 = 8
2. Then add: 3 + 8 = 11
Building the Basics: Simplifying Expressions
Before you can conquer equations, you need to be a master of simplifying expressions. This involves understanding like terms (terms with the same variable raised to the same power), combining these like terms, and using the distributive property.
Combining Like Terms
Imagine you’re organizing a party and you have both red and blue balloons. You wouldn’t mix them up, right? Like terms are similar—only those that share the same variable and exponent can party together! For example, (3x) and (4x) can combine to become (7x), but (3x) and (2y)—nope, they don’t mingle. Another example, (3x) and (5x) are like terms, but (3x) and (3x^2) are not. To simplify, just add or subtract the coefficients of like terms.
Example: 3x + 5x = 8x
The Distributive Property
Using the distributive property might seem tricky, but it’s like spreading peanut butter over your jelly sandwich. To distribute means to multiply something outside the parentheses across all terms inside. So for (2(a + b)), it morphs into (2a + 2b).
Example: 2(x + 3) = 2x + 6
Factoring: The Inverse of Distribution
If you ever reverse that process, that’s factoring! Think of it as asking, “What did I start with before spreading the peanut butter?” So, if you have (6a + 6b), you can factor it back to (6(a + b)).
Example: 2x + 6 = 2(x + 3)
A Crucial Tip: Mastering Operations with Various Number Types

Before we dive into the deep end of equation solving, here's a golden nugget of wisdom: sharpen your skills with all kinds of numbers! You'll often encounter positive and negative numbers, fractions, and decimals when solving equations. They're like the different characters in your math story, each with their own quirks.
Positive and Negative Numbers: These are like the superheroes and villains of the number world. Remember, when you add a negative, it's the same as subtracting a positive. And when you multiply or divide two numbers with the same sign, you get a positive result. Different signs? You're in negative territory!
Fractions: Think of these as pizza slices. Adding or subtracting? Make sure your denominators match first! Multiplying? Just multiply the numerators and denominators separately. Dividing? Flip that second fraction upside down and multiply!
Decimals: These are the sneaky spies of the math world, disguising themselves as parts of whole numbers. Line up those decimal points when adding or subtracting, and don't forget to move the decimal point when multiplying or dividing!
Being comfortable with these different number types is like having a Swiss Army knife in your math toolkit. It'll make your equation-solving journey much smoother. So, practice those operations with all sorts of numbers – your future self will thank you when you're breezing through complex equations!
Tips for Solving and Simplifying Expressions
Now that we're all equipped with the vocab, let’s get down to the nitty-gritty of solving and simplifying expressions.
Get Hands-On with Manipulatives
Numbers can be abstract, so why not make them tangible? When learning to solve equations, (or, really, when learning any new concept) start with concrete representations. Think of manipulatives as your training wheels. In my class, we use Dixie cups and two-color counters to represent different parts of the equation.
I did write a blog for another website where I go over exactly how I use my "cookies and milk" manipulatives to teach solving multistep equations. Feel free to go check out my article titled Unwrapping the Sweet Mystery of Multi-Step Equations: A Fun and Delicious Approach to learn more about how I use manipulatives to solve equations.
Whatever manipulatives you prefer, here’s a game-changing tip: draw a line down the equal sign. This one simple step can transform the way you view equations.
Balance is Key
The golden rule of equations: Whatever you do to one side, you must do to the other. Imagine a balance scale: if you remove one banana from one side, you must remove a banana from the other side to keep it balanced.
Transition from Concrete to Pictorial
Once you're comfortable with manipulatives, move on to drawing pictorial representations. On state tests, you'll often need to interpret or create models of equations. This step is essential for understanding and solving problems. Make sure you can draw these models and, more importantly, understand what they represent.
Go Abstract (But Keep It Real)
Finally, let's talk abstract. What were those manipulatives and drawings actually doing? They were helping you isolate the variable using inverse operations to move everything else to the opposite side of the equation. This is where you really start to feel like a math rockstar
The Power of the Equal Sign Line
Drawing a line down the equal sign helps you see the two sides of the equation as separate entities that must stay balanced. It creates a visual boundary, making it clearer that what happens on one side must be mirrored on the other. This method has turned the light bulb on for many students who were struggling with equations. They start to see the balance and symmetry in equations, and suddenly, things click.
Moving Terms Around: Keeping the Sign
Another super important tip when moving terms around in an equation (which you can do because of the commutative property of addition and multiplication) is to always keep the sign in front of each term with that term. This means you can move 5x + 5 − 3x around as long as you make sure to keep that (-) sign with the 3x
Example: 5x + 5 − 3x → 5x − 3x + 5
This reordering can make the equation easier to work with and is essential for combining like terms correctly.
The Art of Equation Solving: A Step-by-Step Guide
Now that we've armed ourselves with essential vocabulary, let's dive into the actual process of solving equations. Remember, our goal is to isolate the variable—get it all alone on one side of the equation. Here's how we do it:

Draw a vertical line down the equal sign. This visual reminder helps you keep both sides of the equation balanced—what you do to one side, you must do to the other!
Distribute (If needed):Use the distributive property to eliminate parentheses.
Combine Like Terms: Combine like terms on each side of the equation.
Move Variable Terms to One Side: Use addition or subtraction to get all variable terms on one side of the equation and all constant terms on the other side.
Use inverse operations to isolate the variable. Think of this as "undoing" what's been done to the variable.
Addition/Subtraction: Eliminate constant terms by adding or subtracting.
If a number is added to the variable, subtract it from both sides.
If a number is subtracted from the variable, add it to both sides.
Multiplication/Division: Eliminate coefficients by multiplying or dividing.
If the variable is multiplied by a number, divide both sides by that number.
If the variable is divided by a number, multiply both sides by that number.
Check your answer by plugging it back into the original equation.
Remember
There are multiple ways to arrive at the correct answer.
As long as you follow the rules of algebra, you can solve the equation in whichever way you prefer.
This step-by-step guide is a starting point to help you become more comfortable with solving equations.
Let's see this in action with a two-step equation and then a multi-step equation.


Practice Makes Permanent!
Here’s where the fun meets the work! Try these practice problems out for size:
1. Simplify: 3x + 4x - 2x
2. Solve for x: 5x + 2 = 17
3. Solve for x: 3(2x - 7) = 15
(Answers at the end! Feel free to use manipulatives or drawings to help!)
Tips for Success
Practice, Practice, Practice: There’s no substitute for good old-fashioned practice. The more you solve equations, the more confident you’ll become.
Ask for Help: If you’re stuck, don’t be afraid to ask for help. Teachers, tutors, and even online resources can provide the support you need.
Stay Positive: Math can be challenging, but keep a positive attitude. Celebrate your successes and learn from your mistakes.
Solution Awaits!

Math has a knack for feeling overwhelming, but by breaking it down into bite-sized pieces and mixing in some fun, you’ll find yourself armed with the skills needed to conquer any algebraic foe. Remember: every math problem is an adventure waiting for you to solve it. Keep practicing, stay curious, and you’ll soon get those equations under control!
By following these tips, you'll not only master algebraic equations but also impress your teachers, parents, and maybe even your friends. Remember, the goal is to make learning math engaging and fun. If you're looking for personalized help or more tips and tricks, consider booking a free consultation with MindBridge Math Mastery. Let's make math your superpower!
Practice Problems Answer Key:
1. 5x
2. x = 3
3. x = -1
Let the math adventures continue!
Sources:
[1] A Framework for Reflective Practice, https://scholarcommons.usf.edu/cgi/viewcontent.cgi?article=1081&context=jpr
[2] The Importance of a Strong Mathematical Foundation, https://www.semanticscholar.org/paper/0b6e64f4fc0e83a009db6b78b426c2e33a7b110b
[3] Algebra and Art., https://www.semanticscholar.org/paper/63407a334dee1f843fe3f7de6ca6335714a5ecb3




Comments